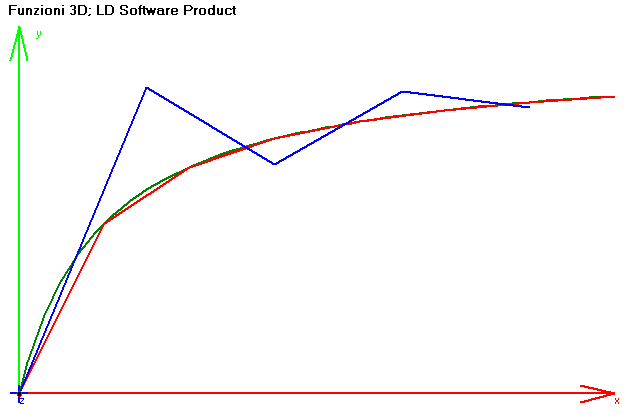
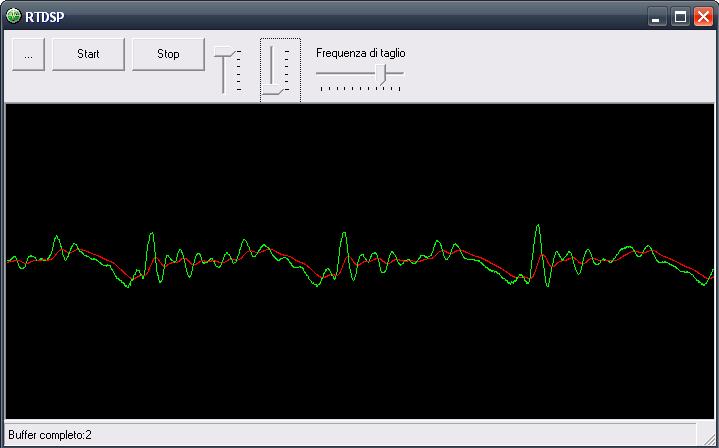
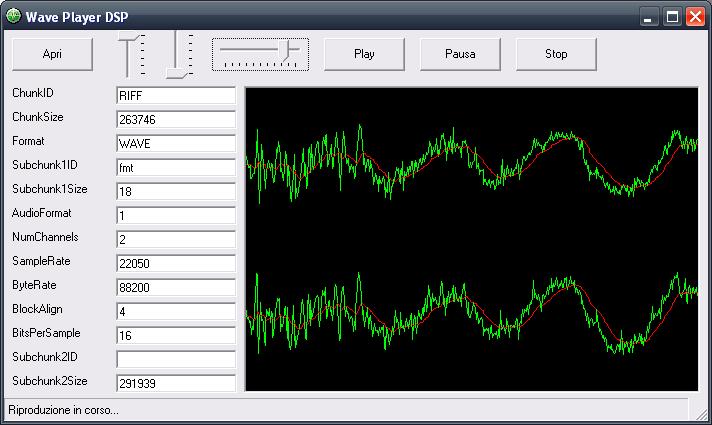
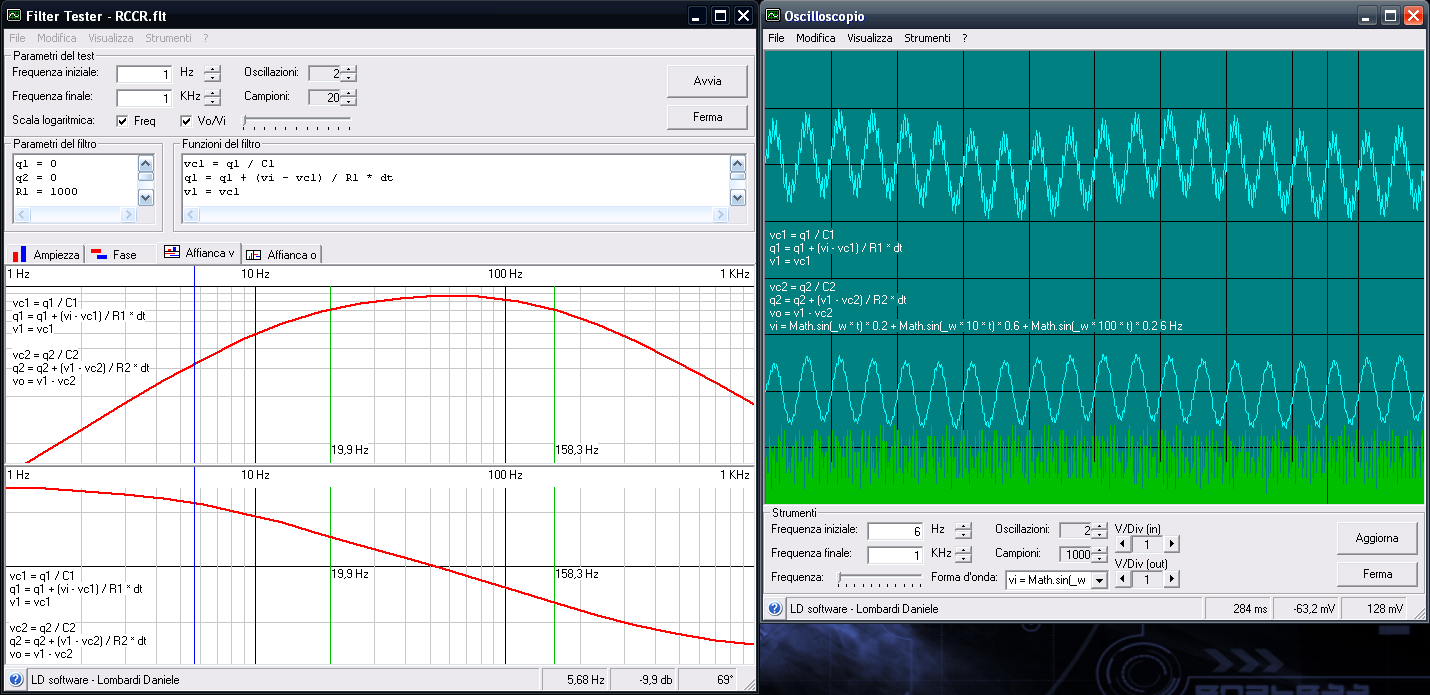
Quella che voglio presentarvi oggi è la mia esperienza fatta nel tentativo (riuscito direi) di realizzare dei filtri digitali, ovvero dei filtri che non sono fatti di componenti elettronici, ma da un algoritmo, implementabili quindi in un pc o in un microcontrollore.

Descrizione

Le notizie che leggerete in questo articolo non sono sconosciute al mondo, semplicemente non sono molto comuni, forse perché quando si sente parlare di analisi di Fourier e numeri immaginari si ci tira subito indietro. Stavolta anche noi comuni mortali che conosciamo poco più delle 4 operazioni riusciremo a capirci qualcosa. Ci tengo a sottolineare che quanto dirò non è tratto da nessun articolo, né deriva da argomenti appresi da qualche parte, l'ho semplicemente "creato" io prima di rendermi conto che qualcuno l'aveva già fatto. Per chi non ha voglia di leggere tutte le formule può andare in fondo alla pagina dove troverà i risultati pronti.

Requisiti

Per comprendere la spiegazione è necessario conoscere la legge di ohm, sapere cos'è un filtro RC, ed avere dimestichezza con le equazioni di primo grado. E' utile avere qualche nozione sul campionamento dei segnali, che mi limiterò a spiegare molto velocemente, per maggiori dettagli vedere qui: campionamento dei segnali.

Considerazioni

Prima di tutto facciamo qualche piccola nota. Un filtro è un'entità capace di trasformare un segnale in un altro, secondo un metodo preciso. Se consideriamo un filtro analogico, esso potrebbe essere un circuito elettronico RC, oppure l'ammortizzatore di un'automobile, mentre se consideriamo un filtro digitale esso è una funzione matematica. Questo non vuol dire che un filtro analogico non possa essere rappresentato da una funzione, anzi, il comportamento dei filtri analogici è proprio la base per costruire i filtri digitali. In elettronica la funzione matematica che descrive il comportamento di un circuito è detta funzione di trasferimento.
Qualunque segnale può essere rappresentato come la successione dei valori che esso assume nel tempo. Per valori si intende l'intensità del segnale (tensione) in un dato istante; per approfondire questo modo rappresentare del segnale, vi rimando alla codifica PCM, che è già ampiamente discussa in rete. Quindi, il nostro filtro sarà una funzione del tipo

Per semplicità indicheremo i segnali con i nomi che si usano generalmente in elettronica:
vi = segnale in ingresso
vo = segnale in uscita
t = tempo

Descrizione

Ora che abbiamo chiarito la simbologia dobbiamo "inventare" la funzione; per farlo, possiamo seguire diverse strade:
1) è intuitivo supporre che fare la media di un segnale equivale ad addolcirlo, ovvero a prenderne solo le componenti a bassa frequenza;
2) ispirarsi ad un modello reale, come un filtro RC;
3) usare le prime due più la propria fantasia per inventarsi di tutto e di più.
In questo tutorial analizzeremo le prime due ed in particolare la seconda per ottimi motivi che vedremo a breve.

1) Metodo della media (FIR)

Come accennato, facendo la media di più valori adiacenti il segnale si addolcisce, il che equivale all'applicazione di un filtro passa basso. Qualcuno si starà chiedendo: “La media restituisce un solo valore, come può questo rappresentare un segnale che varia nel tempo?”. La risposta è che non si tratta di una media normale, ma di una media mobile, ovvero, scelto il numero n di valori di cui fare la media (che in gergo si chiama finestra), per calcolare l’uscita all'istante t bisognerà fare solo la media degli ultimi n valori; ad ogni nuovo istante sposteremo in avanti la finestra (da cui media mobile). Ad ogni valore è possibile associare un peso così da ottenere un effetto diverso (per effetto si intendono la risposta in ampiezza e fase). Facciamo un esempio supponendo di aver scelto n=3:

La media mobile pesata nel campo dei filtri digitali viene chiamata FIR, che sta per Finite Impulse Response, tradotto, Risposta agli Impulsi Finiti, proprio perché viene eseguita elaborando un numero finito di valori (nel nostro esempio 3).

Oltre ai filtri FIR ne esiste un altro tipo, denominato IIR, che sta per Infinite Impulse Response, tradotto, Risposta agli Impulsi Infiniti, la quale tiene conto di tutti i valori assunti dal segnale dall'inizio dell’elaborazione. Qualcuno si starà dicendo: “Sto campionando a 44 KHz, fra 10 secondi ci vorrà un supercomputer per fare una cosa del genere!” Invece, indovinate un po’, un filtro IIR può essere più veloce di uno FIR! Ma analizziamolo nel dettaglio.

2) Riproduzione di un modello reale (IIR)

Questo metodo consiste nel progettare la funzione del filtro semplicemente risolvendo le equazioni di un circuito analogico elettronico. Consideriamo un filtro passa basso di tipo RC: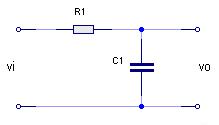

Supponiamo che l’utilizzatore collegato in uscita abbia un’impedenza infinita, di conseguenza in parallelo al condensatore è come se non ci fosse collegato nulla ed il condensatore e la resistenza possono essere considerati collegati in serie con il segnale in ingresso, mentre il segnale in uscita è uguale alla caduta di tensione ai capi del condensatore. Scriviamo le funzioni che ci interessano:

la caduta di tensione ai capi del condensatore è uguale al rapporto tra la carica e la capacità:

la corrente che circola nel circuito in un intervallo di tempo dt è data dal rapporto tra la tensione e la resistenza, ricordando però che il condensatore carico si comporta come una batteria, quindi la sua tensione va sottratta a quella in ingresso:

la carica del condensatore è uguale alla carica nell’istante precedente più la carica che passa in un intervallo di tempo dt; per i matematici:

per i programmatori:

come già detto il segnale in uscita è uguale alla caduta di tensione sul condensatore, quindi

Chi mastica un pochino l’elettronica si accorge subito che c’è qualcosa che non va; la curva di carica del condensatore a tensione costante non è lineare in funzione del tempo, quindi a prima vista la funzione q = q + i * dt sembra sbagliata perché rappresenta una retta.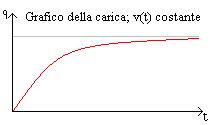

In effetti presa così com’è non è corretta, ma tutti possiamo concordare sul fatto che una curva può essere approssimata con tante piccole rette, quindi se scegliamo un valore di dt molto piccolo e raggiungiamo il risultato attraverso somme successive otteniamo un andamento abbastanza fedele a quello reale. Poiché in genere i segnali vengono campionati ad intervalli di tempo molto piccoli, il nostro requisito risulta naturalmente soddisfatto.
Riassumendo tutto, ad ogni campionamento devono essere eseguite le seguenti operazioni:


q = q + i * dt
vo = vC
Poniamo C=1 (in un circuito RC quello che conta è il prodotto R*C, nessuno ci vieta di porre C=1 e variare soltanto R per modificarne il comportamento) e poniamo K=1/R ottenendo
vC = q
i = (vi - vC) * K
Dal momento che (almeno numericamente) vo=vC e vC=q, possiamo scrivere
vo = vo + i * dt
sostituiamo la corrente con la sua espressione:

eseguiamo il prodotto e mettiamo in evidenza vo:
vo = vo + vi*K*dt – vo*K*dt
vo = vo * (1 - K*dt) + vi*K*dt
se il valore di dt è costante possiamo porre A=K*dt e B=1–K*dt ottenendo

Per come sono definiti i coefficienti la loro somma è sempre uguale a 1, quindi il segnale in uscita non sarà mai più grande del massimo assunto da vi.
Come si può vedere si tratta di una media pesata tra il valore del segnale in uscita precedente e il valore del segnale in ingresso attuale; dal momento che ogni segnale in uscita è funzione di quello precedente il suo valore dipende da tutti i segnali precedenti, quindi abbiamo ottenuto una Risposta agli Impulsi Infiniti, ovvero un filtro IIR.
Quanto minore è il coefficiente A rispetto a B tanto più la frequenza di taglio si abbassa, inquanto il segnale in ingresso ha un peso (A) piccolo.
Per ottenere un filtro passa alto è sufficiente sottrarre dal segnale in ingresso la componente bassa del segnale ottenuta con il filtro appena mostrato; questo risultato trova anche un riscontro elettronico, infatti se osserviamo lo schema di un filtro passa alto di tipo CR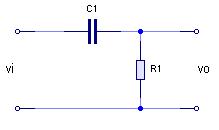

ci accorgiamo che il segnale in uscita non è altro che la caduta di tensione sulla resistenza, ovvero

eseguendo di qui tutti i passaggi otterremmo

da questa relazione si evidenzia inoltre come la somma dei segnali uscenti da un filtro passa basso e uno passa alto calibrati con gli stessi coefficienti A e B dia in uscita il segnale in ingresso

Ricordo che la frequenza di taglio ft di un filtro RC o CR è data da

Visto che abbiamo posto C=1, possiamo riscrivere la frequenza di taglio come

Ricordiamo che avevamo posto K=1/R e A=K*dt, ovvero

Riscriviamo la formula della frequenza di taglio sostituendo 1/R con A e dividendo per dt:

Riscriviamo la formula in funzione di ft:

La frequenza di taglio deve essere al massimo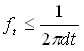

affinchè A e B siano compresi tra 0 e 1. Per poter avere una frequenza di taglio maggiore è necessario che dt sia al massimo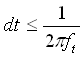

Perché questo? Non avrebbe senso attenuare una frequenza che non si può campionare; ricordiamo infatti che, secondo il teorema di Nyquist, la frequenza massima campionabile è uguale alla metà della frequenza di campionamento (la frequenza di campionamento è l'inverso di dt).

Confronto tra i filtri FIR e IIR

Possiamo osservare che, contrariamente a quanto molti pensano, un filtro IIR richiede in genere meno operazioni di un filtro FIR, infatti un filtro IIR semplice richiede una somma e 2 prodotti, mentre un filtro FIR richiede almeno un prodotto se poniamo tutti i pesi uguali ad uno, ed n-1 somme dove n è il numero degli impulsi da elaborare; tipicamente per ottenere frequenze di taglio molto basse è necessario un numero elevato di campioni.

Tuttavia c’è anche un contro nei filtri IIR, e cioè che essi possono facilmente auto-oscillare, mentre i filtri FIR danno sempre un risultato ben definito.

Cerchiamo di capire perché un filtro IIR oscilla. Supponiamo di applicare in ingresso una tensione costante; dopo un certo tempo il condensatore avrà raggiunto la tensione da noi applicata stabilizzandosi, quindi nel circuito reale non ci sarà auto-oscillazione. Nel paragrafo precedente abbiamo approssimato la curva di carica del condensatore con tante piccole rette, vediamo quindi cosa succede graficamente:

In verde è rappresentata la funzione di carica reale, in rosso la funzione approssimata con dt = 1 e in blu la funzione approssimata con dt = 1.5. Quando dt è troppo grande la retta oltrepassa la curva scavalcandola di volta in volta; come si evince dal grafico il fenomeno è più evidente nel primo tratto della funzione che è proprio la zona di lavoro del filtro. In realtà questo fenomeno risulta evidente solo nei filtri passa-alto quando la frequenza di taglio è prossima al limite calcolato in precedenza.

Filtri di ordine superiore

Per ottenere filtri di ordine superiore, è sufficiente filtrare più volte il segnale con il medesimo filtro, applicando l'uscita di un filtro all'ingresso del successivo. Supponendo di voler realizzare un filtro passa-basso del 3° ordine possiamo scrivere:
vo1 = vo1 * B + vi * A
vo2 = vo2 * B + vo1 * A
vo = vo * B + vo2 * A

Filtri passa banda

Questi filtri si ottengono proprio come si farebbe con un circuito elettronico. Per creare un filtro passa banda è sufficiente creare un filtro passa basso con frequenza di taglio Fsup ed un filtro passa alto con frequenza di taglio Finf, con Finf<Fsup, quindi si applica il primo al segnale in ingresso e il secondo al segnale in uscita dal primo:
Asup = 2 * pi_greco * ftsup * dt
Ainf = 2 * pi_greco * ftinf * dt
Bsup = 1 - Asup
Binf = 1 - Ainf

vo1 = vo1 * Bsup + vi * Asup
vo = vo1 - vo * Binf + vo1 * Ainf

Filtri elimina banda

Anche questi filtri si ottengono proprio come si farebbe con un circuito elettronico. Per creare un filtro elimina banda è sufficiente creare un filtro passa basso con frequenza di taglio Finf ed un filtro passa alto con frequenza di taglio Fsup, con Finf<Fsup, quindi si applicano entrambi i filtri al segnale in ingresso e si sommano i risultati:
Ainf = 2 * pi_greco * ftinf * dt
Asup = 2 * pi_greco * ftsup * dt
Binf = 1 - Ainf
Bsup = 1 - Asup

voInf = voInf * Binf + vi * Ainf
voSup = vi - voSup * Bsup + vi * Asup
vo = voInf + voSup

In alternativa è possibile sottrarre al segnale di ingresso il valore ottenuto con un filtro passa banda calibrato con gli stessi coefficienti.
In generale, se si vuole scomporre un segnale in due componenti, è più conveniente applicare un unico filtro ed ottenere l'altro per complemento.

Costruiamo un equalizzatore

Per costruire un equalizzatore ad n bande è sufficiente applicare n filtri passa banda al segnale in ingresso (devono essere applicati in parallelo non in successione), moltiplicare ciascuno degli n segnali in uscita per un coefficiente Ki e sommare tutti i valori ottenuti. I coefficienti Ki rappresentano l’attenuazione di ogni banda e devono essere compresi tra 0 e 1 (in pratica rappresentano i potenziometri).
Invece di utilizzare n filtri passa banda, è possibile utilizzare un filtro passa basso per la prima banda, ottenere la parte alta per complemento ed applicare un filtro passa basso per la banda successiva. Iterando questi passi è possibile scomporre il segnale con un numero molto ridotto di calcoli.

Un po’ di strumenti

Ok, avete sorbito le mie elucubrazioni fino a questo punto, pensate che vi abbia lasciato solo con un mucchio di parole? Eheh… non mi conoscete bene! Eccovi qualcosa che vi piacerà:

Real Time DSP

Questo è un programma che ho scritto qualche anno fa, consente di elaborare in tempo reale il segnale proveniente dal microfono e di riportarlo in uscita sulle casse. E’ dotato di un equalizzatore a due bande con frequenza di taglio regolabile e visualizza il segnale in ingresso e quello in uscita sullo schermo. E’ possibile modificare alcuni parametri, ma non li toccherei perché è ancora in fase di sviluppo/test. Può essere utilizzato anche come semplice oscilloscopio.

File eseguibile (16 KB)
File eseguibile + librerie per RTDSP o WPDSP (1.94 MB)
Sorgenti (20 KB)

Wave Player DSP

Questo è un programma simile al precedente ma invece di registrare dal microfono consente di aprire un file audio wave della durata massima di 3-4 secondi, pena la vostra vita per caricarlo tutto! Scherzo, ma cercate di non eccedere, anche questo è in fase di sviluppo (e credo che ci resterà per un bel po').

Ho inserito anche un file wave di prova per consentirvi di valutarlo velocemente.
File eseguibile + esempi (261 KB)
File eseguibile + librerie per RTDSP o WPDSP (1.94 MB)
Sorgenti + esempi (254 KB)

Filter Tester

Questo programma vi consentirà di simulare i filtri tracciando i grafici della risposta in frequenza e fase, oltre a visualizzare i segnali sull’oscilloscopio.

Il programma si adatta a qualunque filtro possiate inventarvi, perché utilizza un algoritmo che ottimizza al meglio i tempi di elaborazione senza penalizzare l’affidabilità dei risultati. Ho scritto anche una guida, tuttavia essa è incompleta perché ho fatto delle modifiche/aggiunte che poi non ho avuto tempo di documentare, l’interfaccia comunque è intuitiva e gradevole. All’interno troverete anche alcuni esempi che vi aiuteranno a comprendere meglio il tutorial e l’uso del programma. Per visualizzare la guida contestuale fare click sul pulsante “?” in basso a sinistra e poi cliccare sull’elemento di interesse. Per il momento ho deciso di non pubblicare i sorgenti di questo programma.
File eseguibile + esempi (209 KB)
File eseguibile + esempi + librerie (10.9 MB)

Conclusioni

Come promesso riporto le fantomatiche formule:

Filtro passa basso:
vo = vo * B + vi * A

Filtro passa alto:
vb = vb * B + vi * A
vo = vi - vo

Frequenza di taglio:
A = 2 * pi_greco * ft * dt
B = 1 – A

Spero che abbiate trovato interessante, ma soprattutto utile, questo articolo.

Commento non disponibile per questa notizia.